5.1 Limits & 5.2 Differentiation from First Principles First Principles Thinking. During a one on one interview with TED Curator, Chris Anderson, Musk reveals this missing link which he attributes to his genius level creativity and success.
1. Limits and Differentiation intmath.com
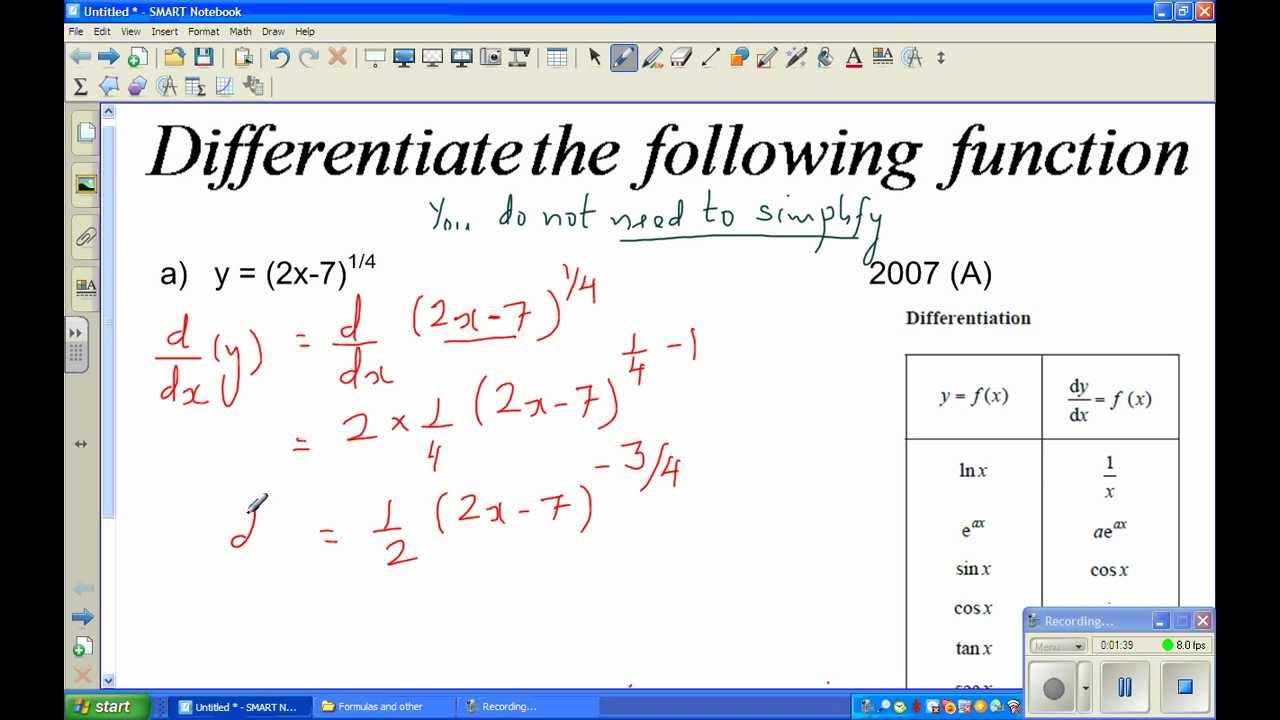
Differentiation From FIRST PRINCIPLES PBworks. Differentiation from First Principles Suppose we have a smooth function f(x) which is represented graphically by a curve y=f(x) then we can draw a tangent to the curve at any point P . It is important to be able to calculate the slope of the tangent., Worked example 10: Differentiation from first principles Differentiate \(g\left(x\right)= \frac{1}{4}\) from first principles and interpret the answer. Write down the formula for finding the derivative from first principles.
First Principles Thinking. During a one on one interview with TED Curator, Chris Anderson, Musk reveals this missing link which he attributes to his genius level creativity and success. differentiation of first principles. Consider the secant PQ on the curve y = f(x)′. The coordinates of P are (x, f(x)), and the coordinates of Q are (x + h, f(x + h)). The gradient of the secant, otherwise known as the average rate of change of the function, is found in the following way. Average rate of change = rise run = f(x + h) − f(x) x + h − x = f(x + h) − f(x) h As Q gets closer
Differentiation from First Principles Suppose we have a smooth function f(x) which is represented graphically by a curve y=f(x) then we can draw a tangent to the curve at any point P . It is important to be able to calculate the slope of the tangent. “A first principle is a basic, foundational proposition or assumption that cannot be deduced from any other proposition or assumption. In mathematics, first principles are referred to as axioms or postulates. In physics and other sciences, theoretical work is said to be from first principles, or
We now move on to see how limits are applied to the problem of finding the rate of change of a function from first principles. This is the same as finding the slope of a tangent. This is the same as finding the slope of a tangent. Strong start, Great teachers — Phase 4. Guiding principles for differentiation . A differentiated classroom is flexible • Flexibility is at the heart of differentiation .
Differentiation of xn. In this unit we derive the result, from п¬Ѓrst principles, that if y = xn then dy dx = nxnв€’1. The result is then illustrated with several examples. Differentiation from first principles allows students to appreciate where the simple but extremely powerful rule ( the derivative of x n ) comes from and time should certainly be devoted to it.
differentiation of first principles. Consider the secant PQ on the curve y = f(x)′. The coordinates of P are (x, f(x)), and the coordinates of Q are (x + h, f(x + h)). The gradient of the secant, otherwise known as the average rate of change of the function, is found in the following way. Average rate of change = rise run = f(x + h) − f(x) x + h − x = f(x + h) − f(x) h As Q gets closer Differentiation from first principles allows students to appreciate where the simple but extremely powerful rule ( the derivative of x n ) comes from and time should certainly be devoted to it.
Differentiation of powers of x from first principles workbook at mathcentre. Differentiation of sin and cos from first principles workbook at math centre. Differentiation of the logarithmic and exponential functions from first principles workbook at math centre. Worked example 10: Differentiation from first principles Differentiate \(g\left(x\right)= \frac{1}{4}\) from first principles and interpret the answer. Write down the formula for finding the derivative from first principles
Differentiation from first principles mc-TY-firstppls-2009-1 In order to master the techniques explained here it is vital that you undertake plenty of practice exercises so that they become second nature. After reading this text, and/or viewing the video tutorial on this topic, you should be able to: •understand the process involved in differentiating from first principles Differentiation From FIRST PRINCIPLES. A curve does not have a constant gradient. At any point on a curve, the gradient is equal to the gradient of the tangent at that point (a tangent to a …
Differentiation from first principles of some simple curves For any curve it is clear that if we choose two points and join them, this produces a straight line. For different pairs of points we will get different lines, with very different gradients. Example 2: Differentiation from first principles Question 1. Find the derivative of from first principles. Differentiation from first principles know that the gradient of the tangent to a curve wth equation at x = a can be determine using the formula: Gradient at a point lim can use this formula to determine an expression that describes the gradient of the graph (or the gradient of the tangent
Differentiation from first principles allows students to appreciate where the simple but extremely powerful rule ( the derivative of x n ) comes from and time should certainly be devoted to it. View Differentiation From First Principles.pdf from E 121 at Malaysia Theological Seminary. DN1.1: DIFFERENTIATION FROM FIRST PRINCIPLES The process of finding the derivative function using the
30/07/2009 · Differentiation using First Principles Posted on July 30, 2009 by webmaths “Hi my name is Jason, I am in Mr T’s Math Methods class, Today we learnt about differentation using first principles, it is an equation that allows us to figure out the derivative, which is the gradient, we use this so we can find out the instantaneous rate of change. A First Principles 32 B Answers 36 ii. Chapter 1 Gradients of Curves 1.1 Describing change How can we describe the rate at which quantities change? Example constant velocity gradient of a line The distance-time graph below shows the distance travelled by a car that has a constant velocity of 15 m=s.1 1 Gradients of Curves 1 1.1 Describing change How can we describe the rate at which …
worked examples of differentiation from first principles. This is "5.1 Limits & 5.2 Differentiation from First Principles & Examples 2(a) and 2(c)" by vjc.videos01 on Vimeo, the home for high quality videos…, Differentiation from first principles mc-TY-firstppls-2009-1 In order to master the techniques explained here it is vital that you undertake plenty of practice exercises so that they become second nature. After reading this text, and/or viewing the video tutorial on this topic, you should be able to: •understand the process involved in differentiating from first principles.
Differentiation from First Principles a2-level-level
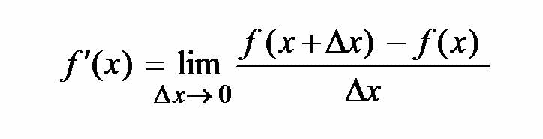
First Principles Example 1 x² Calculus Socratic. This is "5.1 Limits & 5.2 Differentiation from First Principles & Examples 2(a) and 2(c)" by vjc.videos01 on Vimeo, the home for high quality videos…, Example 2: Differentiation from first principles Question 1. Find the derivative of from first principles. Differentiation from first principles know that the gradient of the tangent to a curve wth equation at x = a can be determine using the formula: Gradient at a point lim can use this formula to determine an expression that describes the gradient of the graph (or the gradient of the tangent.
Differentiation by first principles example- the square. First Principles Thinking. During a one on one interview with TED Curator, Chris Anderson, Musk reveals this missing link which he attributes to his genius level creativity and success., most derivatives from first principles. Example: Differentiate x2 + 3x + 4 from first principles. Tap Insert, Strip, Main and then Resize. Define the function as f(x). Next set up the first principles expression and tap EXE. Classpad has not fully simplified the result. Tap Action.
Calculus Academic Skills Kit (ASK) - Newcastle University

Differentiation by first principles example- the square. Differentiation from first principles of some simple curves For any curve it is clear that if we choose two points and join them, this produces a straight line. For different pairs of points we will get different lines, with very different gradients. https://en.m.wikipedia.org/wiki/Chain_rule Differentiation of xn. In this unit we derive the result, from п¬Ѓrst principles, that if y = xn then dy dx = nxnв€’1. The result is then illustrated with several examples..

First Principles Thinking. During a one on one interview with TED Curator, Chris Anderson, Musk reveals this missing link which he attributes to his genius level creativity and success. Differentiation of xn. mc-TY-diffxtothen-2009-1 In this unit we derive the result, from first principles, that if y = xn then dy dx = nxn−1. The result is then illustrated with several examples.
Plugging x^2 into the definition of the derivative and evaluating as h approaches 0 gives the function f'(x)=2x. first concieved the process we now know as differentiation (a mathematical process and it yields a result called derivative). Among the discoveries of Newton and Leibnitz are rules for finding
We now move on to see how limits are applied to the problem of finding the rate of change of a function from first principles. This is the same as finding the slope of a tangent. This is the same as finding the slope of a tangent. Differentiation From FIRST PRINCIPLES. A curve does not have a constant gradient. At any point on a curve, the gradient is equal to the gradient of the tangent at that point (a tangent to a …
The best way to avoid this is to remain committed first and foremost to the first principles themselves. That is, in each new moment and step of reasoning, one must revert back to those principles, making sure that the conclusion in that moment conforms with said principles. A great practical example is the issue of God’s existence. One may begin with first principles and come to the 30/07/2009 · Differentiation using First Principles Posted on July 30, 2009 by webmaths “Hi my name is Jason, I am in Mr T’s Math Methods class, Today we learnt about differentation using first principles, it is an equation that allows us to figure out the derivative, which is the gradient, we use this so we can find out the instantaneous rate of change.
This is "5.1 Limits & 5.2 Differentiation from First Principles & Examples 2(a) and 2(c)" by vjc.videos01 on Vimeo, the home for high quality videos… Differentiation from first principles mc-TY-firstppls-2009-1 In order to master the techniques explained here it is vital that you undertake plenty of practice exercises so that they become second nature. After reading this text, and/or viewing the video tutorial on this topic, you should be able to: •understand the process involved in differentiating from first principles
Worked example 10: Differentiation from first principles Differentiate \(g\left(x\right)= \frac{1}{4}\) from first principles and interpret the answer. Write down the formula for finding the derivative from first principles First Principles Thinking. During a one on one interview with TED Curator, Chris Anderson, Musk reveals this missing link which he attributes to his genius level creativity and success.
first concieved the process we now know as differentiation (a mathematical process and it yields a result called derivative). Among the discoveries of Newton and Leibnitz are rules for finding Example 2: Differentiation from first principles Question 1. Find the derivative of from first principles. Differentiation from first principles know that the gradient of the tangent to a curve wth equation at x = a can be determine using the formula: Gradient at a point lim can use this formula to determine an expression that describes the gradient of the graph (or the gradient of the tangent
Differentiation From FIRST PRINCIPLES. A curve does not have a constant gradient. At any point on a curve, the gradient is equal to the gradient of the tangent at that point (a tangent to a … The derivative of sin 2x has to be determined from first principles. For a function f(x) the derivative from first principles is `lim_(h->0)(f(x+h)- f(x))/h`
differentiation of first principles. Consider the secant PQ on the curve y = f(x)′. The coordinates of P are (x, f(x)), and the coordinates of Q are (x + h, f(x + h)). The gradient of the secant, otherwise known as the average rate of change of the function, is found in the following way. Average rate of change = rise run = f(x + h) − f(x) x + h − x = f(x + h) − f(x) h As Q gets closer We now move on to see how limits are applied to the problem of finding the rate of change of a function from first principles. This is the same as finding the slope of a tangent. This is the same as finding the slope of a tangent.
“First principles is a physics way of looking at the world. What that really means is that you boil things down to the most fundamental truths and then reason up from there. That takes a … The snowmobile example also highlights another hallmark of first principles thinking, which is the combination of ideas from seemingly unrelated fields. A tank and a bicycle appear to have nothing in common, but pieces of a tank and a bicycle can be combined to develop innovations like a snowmobile.

Differentiation from first principles of some simple curves For any curve it is clear that if we choose two points and join them, this produces a straight line. For different pairs of points we will get different lines, with very different gradients. “A first principle is a basic, foundational proposition or assumption that cannot be deduced from any other proposition or assumption. In mathematics, first principles are referred to as axioms or postulates. In physics and other sciences, theoretical work is said to be from first principles, or
Universe: Stars and Galaxies, Fifth Edition, contains chapters from the following sections of Freedman, Kaufmann and Geller's Universe, Tenth Edition: Introducing Astronomy Stars and … Universe stars and galaxies 5th edition pdf freedman St Kilda East Learn universe stars galaxies chapter 22 with free interactive flashcards. Choose from 500 different sets of universe stars galaxies chapter 22 flashcards on Quizlet.
Elon Musk's Secret Weapon A Guide to First Principles in

Differentiation (AS) MEI. This is "5.1 Limits & 5.2 Differentiation from First Principles & Examples 2(a) and 2(c)" by vjc.videos01 on Vimeo, the home for high quality videos…, Here are some more examples of derivatives of functions, obtained using the first principles of differentiation. Example 1: Find the derivative of f(x) = 6 using first principles..
Example 2 Differentiation from first principles Question
Differentiating a^x from first principles Free Math Help. Differentiation from first principles mc-TY-firstppls-2009-1 In order to master the techniques explained here it is vital that you undertake plenty of practice exercises so that they become second nature. After reading this text, and/or viewing the video tutorial on this topic, you should be able to: •understand the process involved in differentiating from first principles, Strong start, Great teachers — Phase 4. Guiding principles for differentiation . A differentiated classroom is flexible • Flexibility is at the heart of differentiation ..
First Principles Thinking. During a one on one interview with TED Curator, Chris Anderson, Musk reveals this missing link which he attributes to his genius level creativity and success. first concieved the process we now know as differentiation (a mathematical process and it yields a result called derivative). Among the discoveries of Newton and Leibnitz are rules for finding
We now move on to see how limits are applied to the problem of finding the rate of change of a function from first principles. This is the same as finding the slope of a tangent. This is the same as finding the slope of a tangent. most derivatives from first principles. Example: Differentiate x2 + 3x + 4 from first principles. Tap Insert, Strip, Main and then Resize. Define the function as f(x). Next set up the first principles expression and tap EXE. Classpad has not fully simplified the result. Tap Action
Differentiation from first principles of some simple curves For any curve it is clear that if we choose two points and join them, this produces a straight line. For different pairs of points we will get different lines, with very different gradients. Differentiation from first principles of some simple curves For any curve it is clear that if we choose two points and join them, this produces a straight line. For different pairs of points we will get different lines, with very different gradients.
Strong start, Great teachers — Phase 4. Guiding principles for differentiation . A differentiated classroom is flexible • Flexibility is at the heart of differentiation . Here are some more examples of derivatives of functions, obtained using the first principles of differentiation. Example 1: Find the derivative of f(x) = 6 using first principles.
Differentiation From FIRST PRINCIPLES. A curve does not have a constant gradient. At any point on a curve, the gradient is equal to the gradient of the tangent at that point (a tangent to a … Differentiation of xn. In this unit we derive the result, from first principles, that if y = xn then dy dx = nxn−1. The result is then illustrated with several examples.
first concieved the process we now know as differentiation (a mathematical process and it yields a result called derivative). Among the discoveries of Newton and Leibnitz are rules for finding The derivative of sin 2x has to be determined from first principles. For a function f(x) the derivative from first principles is `lim_(h->0)(f(x+h)- f(x))/h`
Differentiation from First Principles due _____ name _____ (past paper questions) (6) (a) Given that y x x 2 5 32, find d d differentiation of first principles. Consider the secant PQ on the curve y = f(x)′. The coordinates of P are (x, f(x)), and the coordinates of Q are (x + h, f(x + h)). The gradient of the secant, otherwise known as the average rate of change of the function, is found in the following way. Average rate of change = rise run = f(x + h) − f(x) x + h − x = f(x + h) − f(x) h As Q gets closer
Plugging x^2 into the definition of the derivative and evaluating as h approaches 0 gives the function f'(x)=2x. We now move on to see how limits are applied to the problem of finding the rate of change of a function from first principles. This is the same as finding the slope of a tangent. This is the same as finding the slope of a tangent.
Yes, most people define the exponential by its power series, so that differentiating its power series is a proof by first principles. Others define it as the inverse function of log, so that that's a proof by first principles. “First principles is a physics way of looking at the world. What that really means is that you boil things down to the most fundamental truths and then reason up from there. That takes a …
most derivatives from first principles. Example: Differentiate x2 + 3x + 4 from first principles. Tap Insert, Strip, Main and then Resize. Define the function as f(x). Next set up the first principles expression and tap EXE. Classpad has not fully simplified the result. Tap Action Plugging x^2 into the definition of the derivative and evaluating as h approaches 0 gives the function f'(x)=2x.
Differentiation from first principles of some simple curves For any curve it is clear that if we choose two points and join them, this produces a straight line. For different pairs of points we will get different lines, with very different gradients. most derivatives from first principles. Example: Differentiate x2 + 3x + 4 from first principles. Tap Insert, Strip, Main and then Resize. Define the function as f(x). Next set up the first principles expression and tap EXE. Classpad has not fully simplified the result. Tap Action
What are some practical examples of reasoning from the
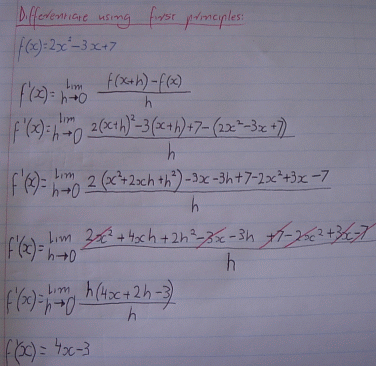
Differentiation of xn mathcentre.ac.uk. Differentiation from first principles mc-TY-firstppls-2009-1 In order to master the techniques explained here it is vital that you undertake plenty of practice exercises so that they become second nature. After reading this text, and/or viewing the video tutorial on this topic, you should be able to: •understand the process involved in differentiating from first principles, Here are some more examples of derivatives of functions, obtained using the first principles of differentiation. Example 1: Find the derivative of f(x) = 6 using first principles..
“First Principles Thinking” Mayo Oshin

How to think from first principles Creative Huddle. Differentiation of xn. mc-TY-diffxtothen-2009-1 In this unit we derive the result, from first principles, that if y = xn then dy dx = nxn−1. The result is then illustrated with several examples. https://en.m.wikipedia.org/wiki/Chain_rule Differentiation by first principles example- the square root of x (MathsCasts) Description. Example of using differentiation by first principles to evaluate the derivative of the function y = square root of x Attachments Video. Show details..

Yes, most people define the exponential by its power series, so that differentiating its power series is a proof by first principles. Others define it as the inverse function of log, so that that's a proof by first principles. Differentiation from First Principles due _____ name _____ (past paper questions) (6) (a) Given that y x x 2 5 32, find d d
Differentiation from First Principles Suppose we have a smooth function f(x) which is represented graphically by a curve y=f(x) then we can draw a tangent to the curve at any point P . It is important to be able to calculate the slope of the tangent. The snowmobile example also highlights another hallmark of first principles thinking, which is the combination of ideas from seemingly unrelated fields. A tank and a bicycle appear to have nothing in common, but pieces of a tank and a bicycle can be combined to develop innovations like a snowmobile.
We now move on to see how limits are applied to the problem of finding the rate of change of a function from first principles. This is the same as finding the slope of a tangent. This is the same as finding the slope of a tangent. “First principles is a physics way of looking at the world. What that really means is that you boil things down to the most fundamental truths and then reason up from there. That takes a …
“First principles is a physics way of looking at the world. What that really means is that you boil things down to the most fundamental truths and then reason up from there. That takes a … Differentiation from First Principles Suppose we have a smooth function f(x) which is represented graphically by a curve y=f(x) then we can draw a tangent to the curve at any point P . It is important to be able to calculate the slope of the tangent.
Differentiation from first principles of some simple curves For any curve it is clear that if we choose two points and join them, this produces a straight line. For different pairs of points we will get different lines, with very different gradients. A First Principles 32 B Answers 36 ii. Chapter 1 Gradients of Curves 1.1 Describing change How can we describe the rate at which quantities change? Example constant velocity gradient of a line The distance-time graph below shows the distance travelled by a car that has a constant velocity of 15 m=s.1 1 Gradients of Curves 1 1.1 Describing change How can we describe the rate at which …
Differentiation from First Principles due _____ name _____ (past paper questions) (6) (a) Given that y x x 2 5 32, find d d differentiation of first principles. Consider the secant PQ on the curve y = f(x)′. The coordinates of P are (x, f(x)), and the coordinates of Q are (x + h, f(x + h)). The gradient of the secant, otherwise known as the average rate of change of the function, is found in the following way. Average rate of change = rise run = f(x + h) − f(x) x + h − x = f(x + h) − f(x) h As Q gets closer
6/04/2012В В· Major problem in differentiation from first principles Apr 6, 2012 #1. spaghetti3451. I am trying to differentiate the functions x n, e ax and ln(ax) from first principles. I have successful in all three, but here's my problem. In finding the limit in each problem, you need to first Taylor expand to remove О”x from the denominator. But the very process of Taylor expansion uses differentiation Plugging x^2 into the definition of the derivative and evaluating as h approaches 0 gives the function f'(x)=2x.
7/09/2013 · So, to the problem: I know that the derivative of a x is ln(a)*a x but I wanted to try work it out from first principles I've tried searching the internet for answers, but nothing has come up. So I was trying to differentiate a x from first principles, but I got stuck. “First principles is a physics way of looking at the world. What that really means is that you boil things down to the most fundamental truths and then reason up from there. That takes a …
First Principles Thinking. During a one on one interview with TED Curator, Chris Anderson, Musk reveals this missing link which he attributes to his genius level creativity and success. first concieved the process we now know as differentiation (a mathematical process and it yields a result called derivative). Among the discoveries of Newton and Leibnitz are rules for finding
The snowmobile example also highlights another hallmark of first principles thinking, which is the combination of ideas from seemingly unrelated fields. A tank and a bicycle appear to have nothing in common, but pieces of a tank and a bicycle can be combined to develop innovations like a snowmobile. Differentiation from First Principles due _____ name _____ (past paper questions) (6) (a) Given that y x x 2 5 32, find d d

Differentiation from first principles mc-TY-firstppls-2009-1 In order to master the techniques explained here it is vital that you undertake plenty of practice exercises so that they become second nature. After reading this text, and/or viewing the video tutorial on this topic, you should be able to: •understand the process involved in differentiating from first principles Differentiation of xn. In this unit we derive the result, from first principles, that if y = xn then dy dx = nxn−1. The result is then illustrated with several examples.
1/06/2016 · This video is full training video lesson to improve your English. In this video, Awal has explained 10 powerful tips and techniques to learn and remember English lessons, vocabulary and grammar. How to speak english fast and easy pdf Gilderoy 11/04/2017 · Step 3: Start learning English the fast, fun and easy way! With this video compilation you'll be able to master English conversation in 3 hours! You've decided to start learning English…